Statistical Learning Notes | SVM 1 - HyperPlane, Support Vectors and Maximal Margin Classification

SVM 1. Maximal Margin Classifier

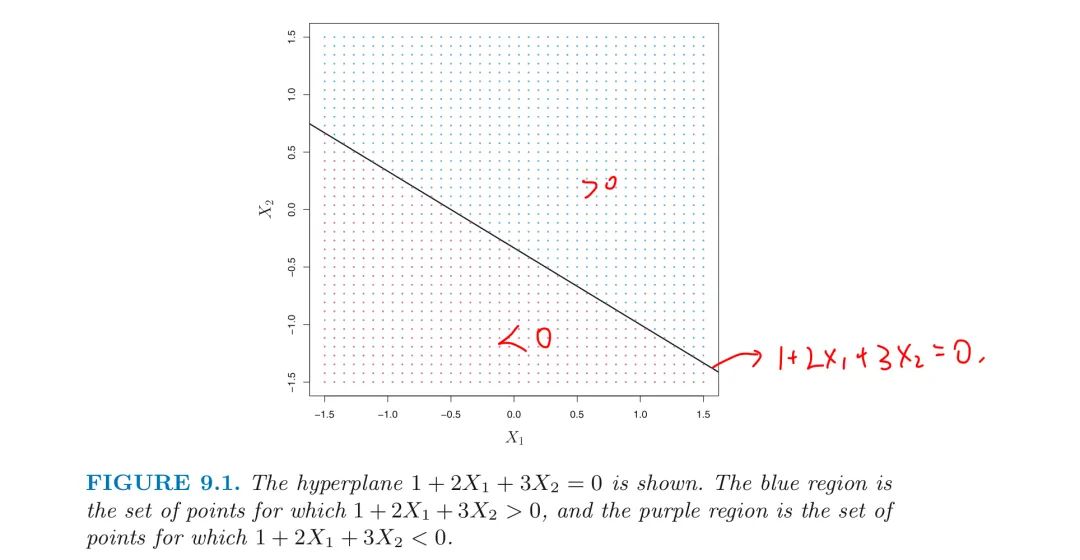
1.1. What is a HyperPlane?

Definition: In a p-dimensional space, a HyperPlane is a flat affine subspace of dimension p-1

• affine: the subspace need not pass through the origin
• if $p=2$, a hyperplane is a flat 1-dimensional subspace
  • in other words, a Line => $\beta_0 + \beta_1X_1 + \beta_2X_2 = 0$
• if $p=3$, a hyperplane is a flat 2-dimensional subspace
  • in other words, a Plane

If $p>3$: the p-dimensional hyperlane is defined by the equation: $$\beta_0 + \beta_1X_1 + \beta_2X_2 + … + \beta_pX_p= 0$$

• if a point $X=(X_1, X_2, …, X_p)^T$ in p-dimensional space (i.e. a vector of length p) satisfies the above equation
  • then X lies on the hyperplane
  • otherwise, X lies on the one of two sides of the hyperplane
    • we can think of the hyperplane as dividing p-dimensional space into two halves

1.2. Classification using a Separating HyperPlane

Suppose that we have a $n \times p$ data matrix $X$

• that consists of n training observations in p-dimensional space

$$ x_1 = \begin{pmatrix} x_{11} \
\vdots \
x_{1p} \end{pmatrix} $$

• and these n observations fall into two classes:

$$ y_1, \cdots, y_n \in { -1,1 } $$

A classifier that is based on a separating hyperplane leads to a linear decision boundary

• for a test observation, calculate $f\relax{x^{*}}=\beta_0 + \beta_1X_1 + \beta_2X_2 + … + \beta_pX_p$
  • if $f(x^*)$ is positive, then we assign the test data to class 1
  • if $f(x^*)$ is negative, then we assign the test data to class -1
  • if $|f(x^*)|$ is far from 0, we can be confident about the class assignment
  • if $|f(x^)|$ is close to 0, we are less certain about the class assignment for $x^{}$

1.3. Construction of Maximal Margin Classifier

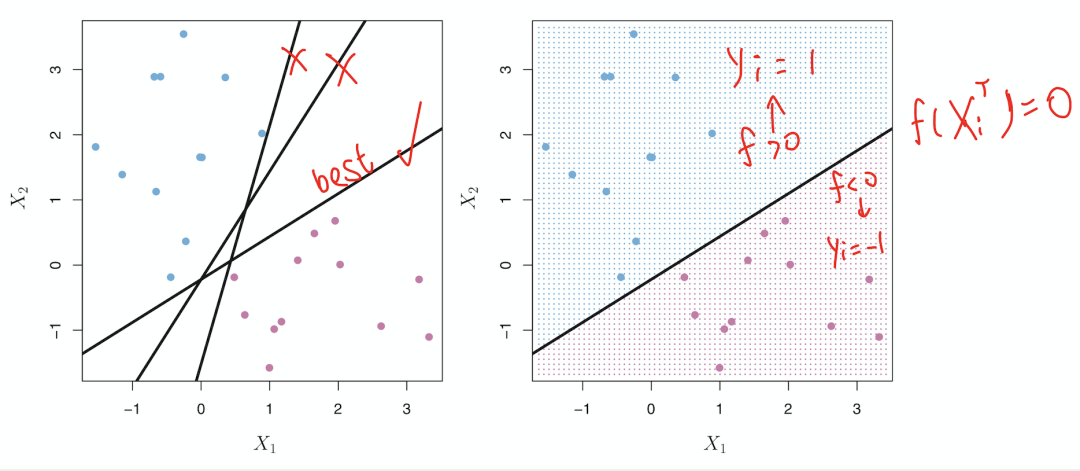
In general, there will exist inifinite number of hyperplane

• if the data can be perfectly separated using a hyperplane
• three of inifinite possible separating hyperlanes are shown in the left-hand panel of above figure

Maximal Margin Hyperplane is the optimal choice

• which is the separating hyperplane that is farthest from the training observations
• Margin: the smallest (perpendicular) distance of all training observations to a given separating hyperplane
• In a sense, the maximal margin hyperplane represents the mid-line of the widest “slab”
  • that we can insert between the two classes

Support Vectors:
The training observations that are equidistant from the Maximal Margin Hyperplane and lies along the width of the margin

• they “support” the Maximal Margin Hyperplane since if these points of support vectors were moved slightly then the Maximal Hyperplane would move as well!!!
  • property for later SVC and SVM: the maximal margin hyperplane depends directly on ONLY a small subset of observations (support vectors)

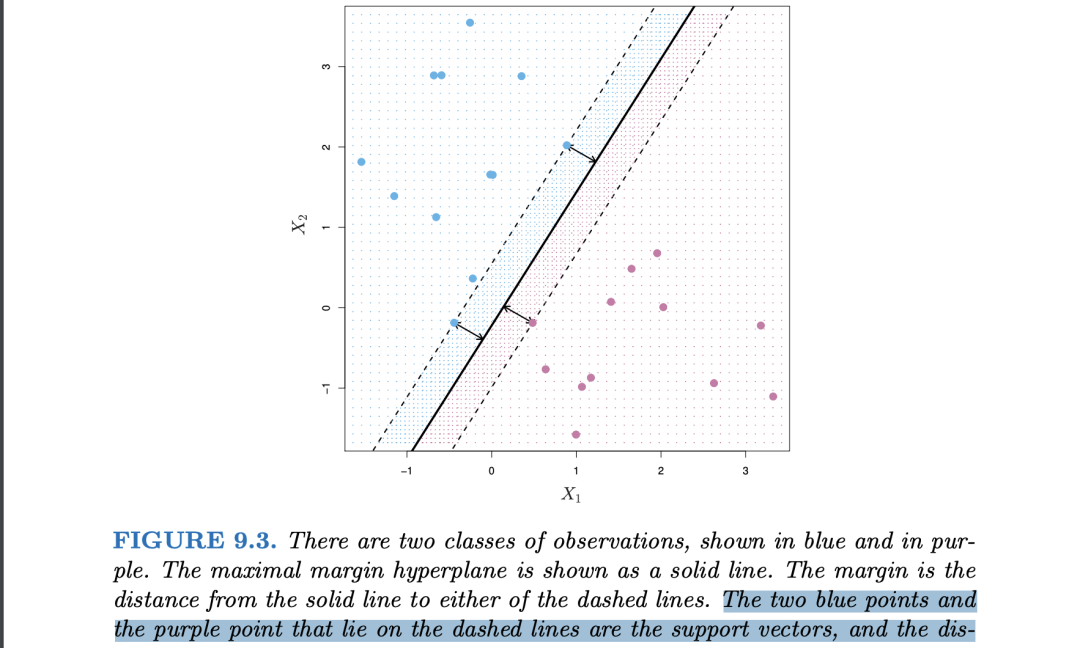
The Maximal Margin Hyperplane is the solution to the constrained optimization problem :

• M represents the margin of hyperplane

$$\max_{\beta_0,\beta_1,\cdots,\beta_p,M} M$$ $$s.t. \sum_{j=1}^p \beta_j^2 = 1$$ $$y_i(\beta_0 + \sum_{k=1}^p\beta_kx_{ik})\geq M$$ $$for \ i = 1, \cdots, n$$

• the constraints ensure that each observation is on the correct side of the hyperlane and at least a distance M from the hyperplane

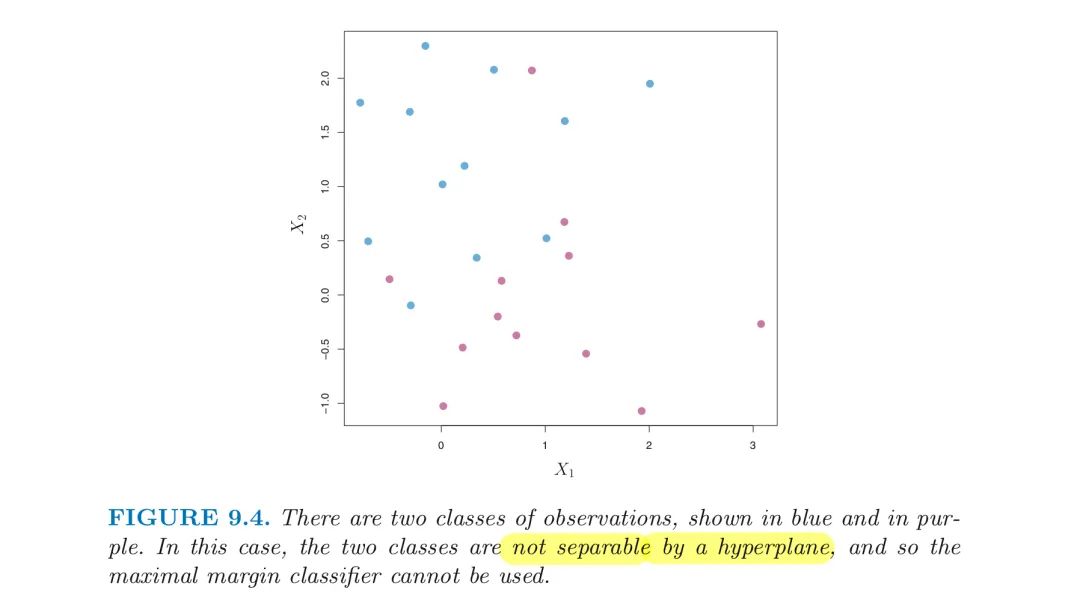
1.4 The Non-Separable Case

In many cases NO separating hyperplane exists, and so there is NO Maximal Margin Classifier.

• the optimization problem has NO solution with M > 0.

Next: Support Vector Classifier The generalization of the Maximal Margin Classifier to the Non-Separable Case

• that can develop a hyperplane that almost separates the classes
• using soft margin