Statistical Learning Notes | LDA 1 - Linear Discriminant Analysis
ISLR4.4 - LDA
0. LDA vs Logistic Regression
- When the classes are well-separated, the parameter estimates for the logistic regression model are surprisingly unstable
- LDA is more stable than Logistic Regression
- If n is small and distribution X ~ Normal in each of the classes,
- LDA is more accurate than Logistic Regression
- LDA is more common when we have more than two response classes ($K \geq 2 $ )
- because it also provides low-dimensional views of the data
1. Bayes' Theorem for Classification
Modeling the distribution of X in each of the classes separately,
- and then use Bayes Theorem to flip things around and obtain $Pr(Y|X)$
Using Normal(Gaussian) distributions for each class,
- leads to Linear or Quadratic Discriminant Analysis
Bayes Theorem for LDA:
Let $\pi_k$ represent the prior probability
- that a randomly chosen observation comes from the kth class;
Let $f_k(x)=\Pr(X=x|Y=k)$ denote the density function of X
-
for an observation that comes from the kth class.
-
larger $f_k(x)$ => higher probability that an observation in the kth class has $X\approx x$
-
$\Pr(Y=k\ |\ X=x)=\frac{Pr(Y=k) · Pr(X=x|Y=k)}{Pr(X=x)}$ $$\Downarrow$$ $$p_k(x)=\frac{\pi_kf_k(x)}{\sum_{l=1}^K\pi_lf_l(x)}$$
-
$p_k(x)=\Pr(Y=k\ |\ X=x)$ is the posterior probability that an observation $X=x$ belongs to the kth class
Estimating $\pi_k$ is Easy if we have a random sample from the population:
- simply compute the fraction of the training observations that belong to the kth class
Estimating $f_k(x)$ is Challenging
- have to make some simplifying assumptions
- LDA, QDA and Naive Bayes are three classifiers that use different estimates of $f_k(x)$ to approximate the Bayes classifier
2. LDA for Single Predictor
LDA Classifier results from assuming that $f_k(k)$ has the form of Normal (Gaussian) Density:
$$f_k(x)=\frac{1}{\sqrt{2\pi} \ \sigma_k}\exp{(-\frac{1}{2\sigma_k^2}(x-\mu_k)^2)}$$
- $\mu_k$ is the mean, $\sigma_k^2$ is the variance in class k
- assume that all $\sigma_k^2 = \sigma^2$ are the same
- different class-specific variance => QDA
So the posterior probability is: $$p_k(x)=\frac{\pi_k \frac{1}{\sqrt{2\pi} \sigma}e^{(-\frac{1}{2\sigma^2}(x-\mu_k)^2)}}{\sum_{l=1}^K \pi_l \frac{1}{\sqrt{2\pi} \sigma}e^{(-\frac{1}{2\sigma^2}(x-\mu_l)^2)}}$$
- The Bayes Classifier involves assigning an observation $X = x$ to the class for which $p_k(x)$ is Largest
- Simplify: Taking Logs, and discarding terms that do not depend on k, we simplify the goal to get the Largest Discriminant Score
$$\delta_k(x)=x\cdot\frac{\mu_k}{\sigma^2}-\frac{\mu_k^2}{2\sigma^2}+\ln(\pi_k)$$
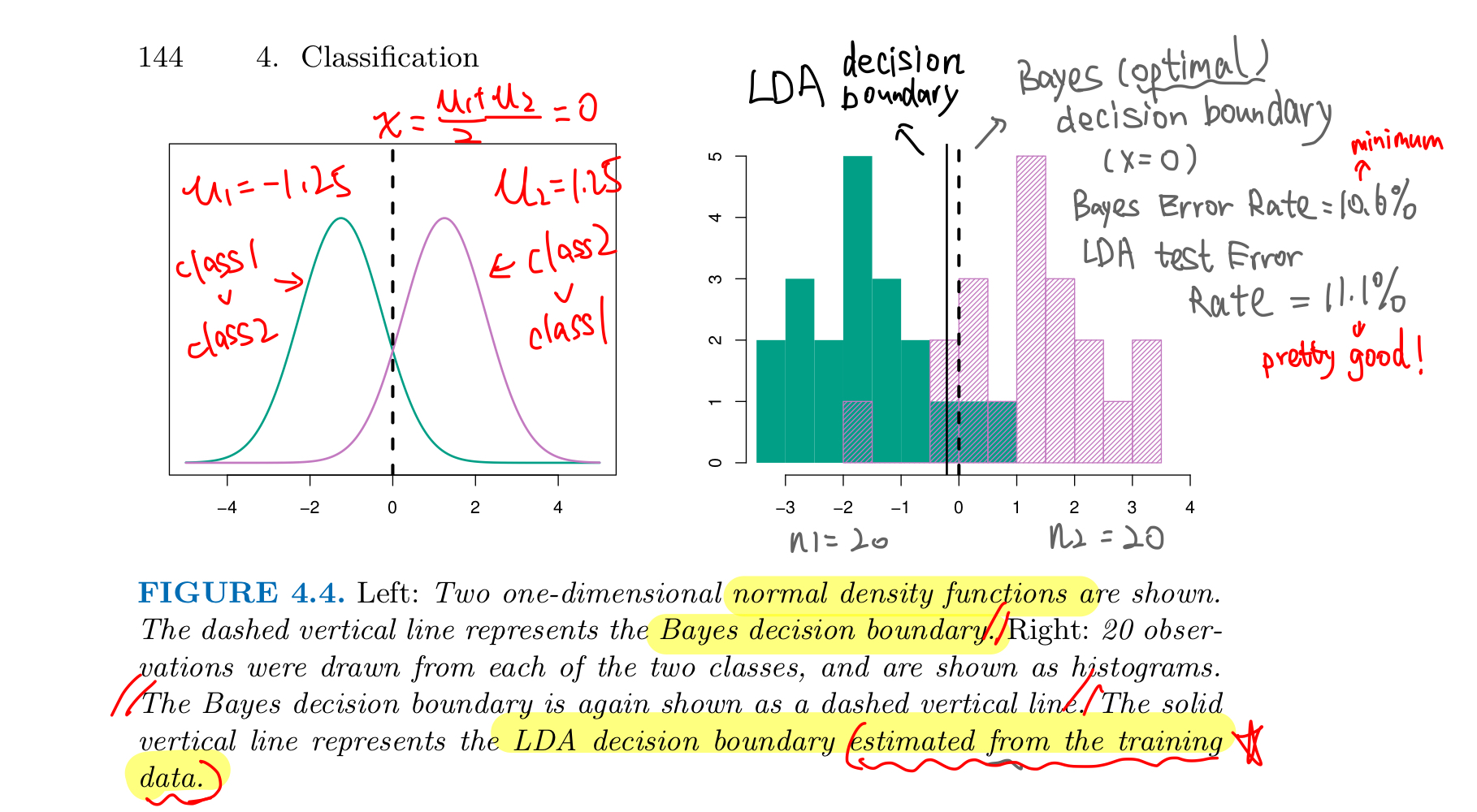
Example
If K = 2, and $\pi_1=\pi_2=0.5$, the Bayes decision boundary is at $$x = \frac{\mu_1^2-\mu_2^2}{2(\mu_1-\mu_2)}=\frac{\mu_1+\mu_2}{2}$$
- Let $\mu_1 = -1.25, \mu_2=1.25 \ and \ \sigma=1$, Bayes classifier
- assigns class 1 if x < 0
- assigns class 2 if x > 0
In real-life we don’t know the distribution and parameters, we JUST have the training data
- not able to calculate the Bayes Classifier
- need to estimate the parameters and approximate the optimal Bayes Classifier
Estimating the Parameters
The LDA method approxiates the Bayes Classifier by using the following estimates:
$$\hat{\pi}k=n_k/n$$
$$\hat{\mu}k=\frac{1}{n_k}\sum{i:y_i-k}x_i$$
$$\hat{\sigma}^2=\frac{1}{n-K}\sum^K{k=1}\sum_{i:y_i=k}(x_i-\hat{\mu}_k)^2$$
$$=\sum_{k=1}^K\frac{n_k-1}{n-K}\cdot\hat{\sigma}_k^2$$
where estimated variance in the kth class
$$\hat{\sigma}_k^2=\frac{1}{n_k-1}\sum_{i:y_i=k}(x_i-\hat{\mu}_k)^2$$
- LDA estimates $\pi_k$ using the proportion of the training observations that belong to the kth class
- the estimate for $\mu_k$ is the average of all the training data from the kth class
- $\hat{\sigma}^2$ can be seen as a weighted average of the sample variances for each of the K classes.
Discriminant Functions
LDA classifiers plugs the estimates given above into the discriminant functions $\delta_k(x)$ $$\hat{\delta}_k(x)=x\cdot\frac{\hat{\mu}_k}{\hat{\sigma}^2}-\frac{\hat{\mu}_k^2}{2\hat{\sigma}^2}+\ln(\hat{\pi}_k)$$
- and _assigns an observation X=x to the class k for which $\hat{\delta}k(x)$ is largest
- $\hat{\delta}_k(x)$ are linear functions of x
Evaluation
3. LDA for Multiple Predictors
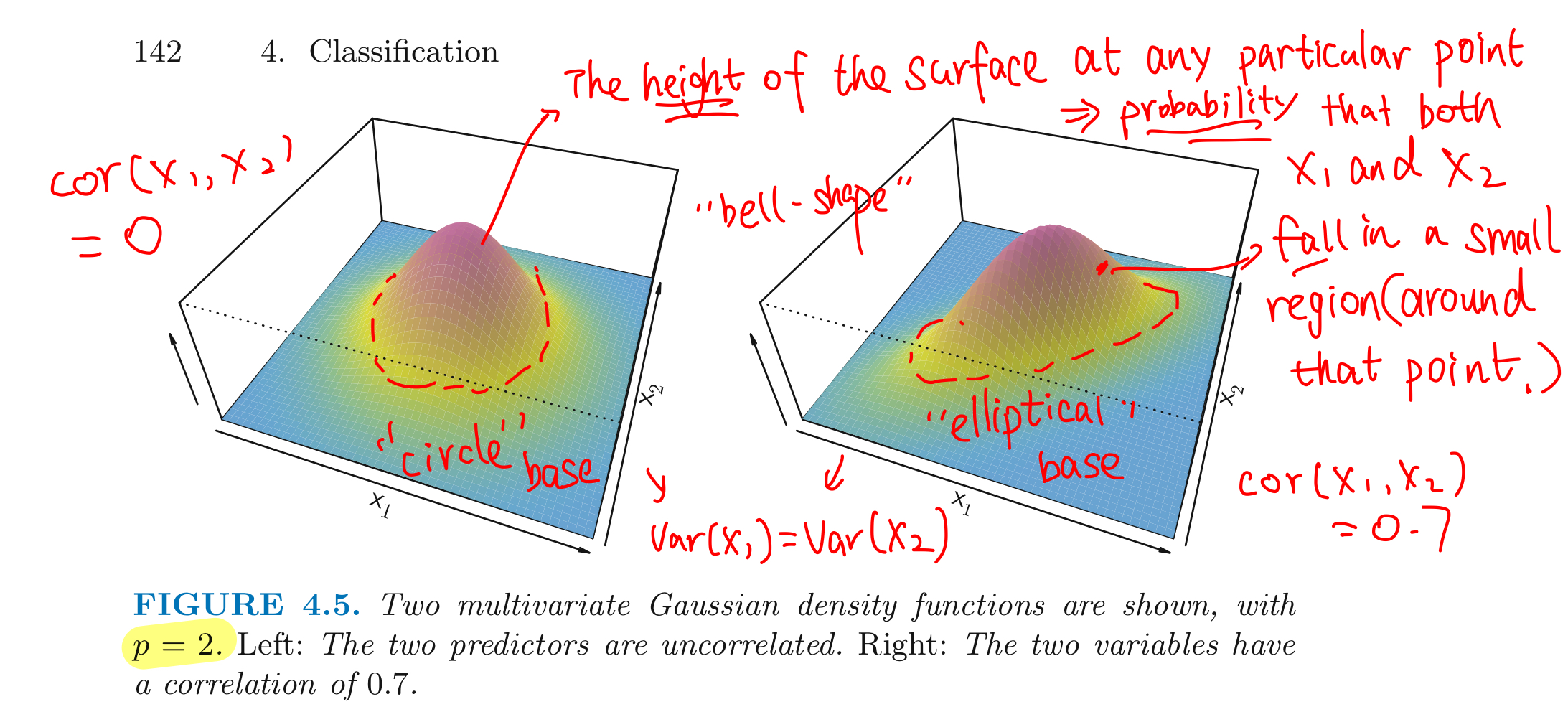
Assume that $X=(X_1,X_2,\cdots,X_p) $ in the kth class is drawn from a MultiVariate Gaussian (normal) Distribution, $X \sim N(\mu_k,\Sigma)$:
$$f_k(x)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))}$$
- $\mu_k=E(X)$ is a class-specific mean vector of X
- $\Sigma = Cov(X)$ is the $p \times p$ covariance matrix that is common to ALL K classes
MultiVariate Gaussian Distribution assumes that each individual predictor follows a 1-dimensional normal distribution
- with some correlation between each pair of predictors
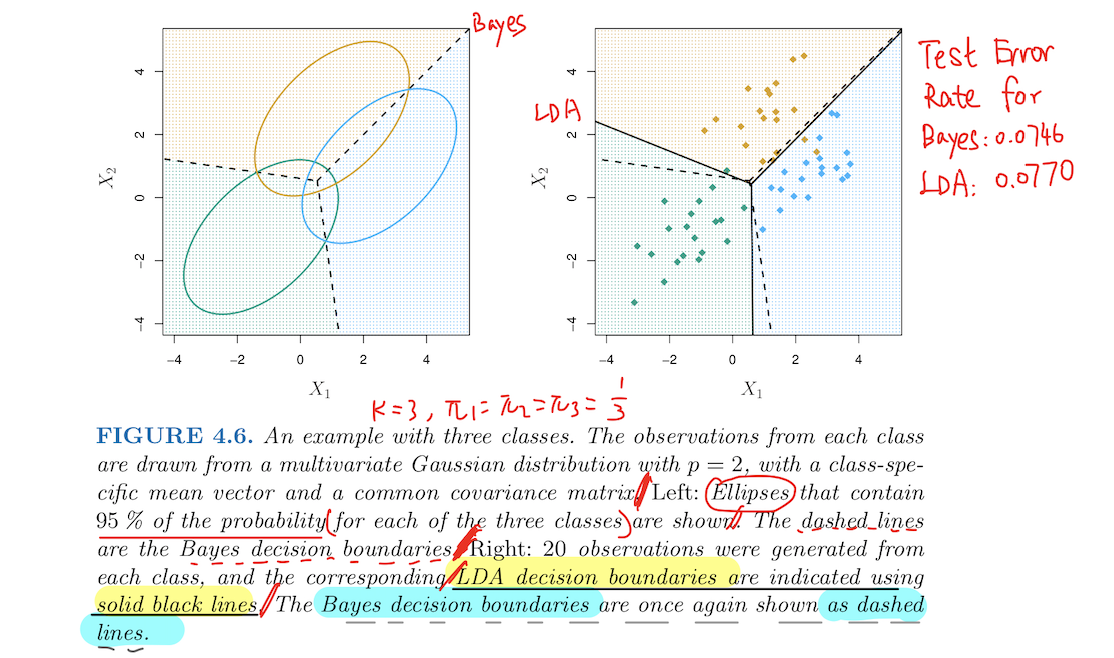
Plugging the density function for the kth class, $f_k(X=x)$ into Bayes Theorem and performing algebra reveals that
- Bayes Classifier assigns an observation X=x to the class for which the Discriminant function is largest: $$\delta_k(x)=x^T\Sigma^{-1}\mu_k-\frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k+\log\pi_k$$
- by Estimating unknown Parameters in the same way in 1-dim case
Next:
LDA on Credit Dataset, ROC, AUC