Deep Learning Notes 04 | Weight Initialization and Gradient Check for DNN

1. Weight Initialization

A well chosen initialization can:

• Speed up the convergence of gradient descent
• Increase the odds of gradient descent converging to a lower training (and generalization) error

Gradient Exploding and Vanishing

Training a neural network requires specifying an initial value of the weights. A well chosen initialization method will help learning.

• if W > I (Identity Matrix): in DNN, the activations can explode
• if W < I: the activations will decrease exponentially and then vanish

Zero Initialization：

• this will fail to classify

1
2
3
4
5
6
7
8
9

def initialize_parameters_zeros(layers_dims):

    parameters = {}
    L = len(layers_dims)            # number of layers in the network

    for l in range(1, L):
        parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1]))
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

Output:

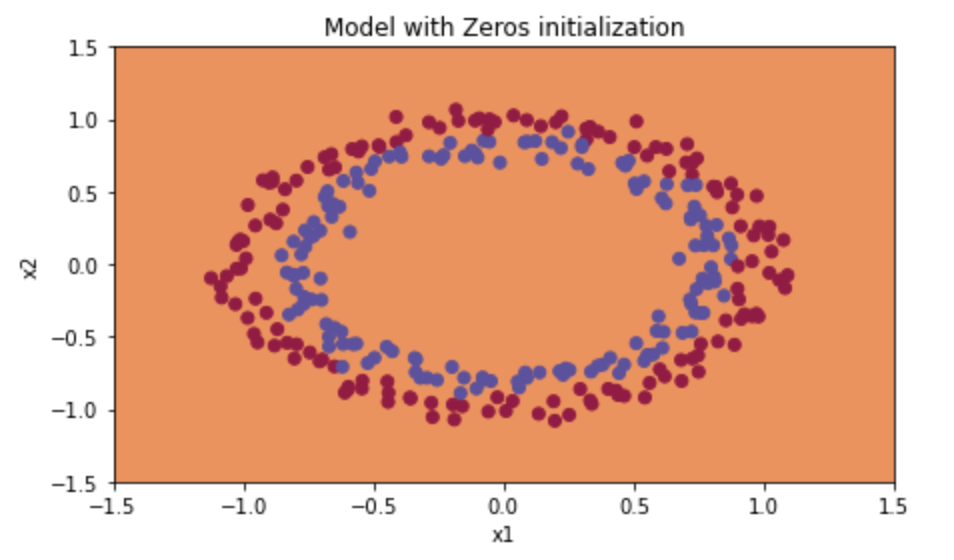
• Train Accuracy: 50%

Random Initialization:

Poor initialization can lead to vanishing/exploding gradients, which also slows down the optimization algorithm.

• parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*10
• parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def initialize_parameters_random(layers_dims):

    np.random.seed(3)               # This seed makes sure your "random" numbers will be the as ours
    parameters = {}
    L = len(layers_dims)            # integer representing the number of layers

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*10
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))

    return parameters

Output:

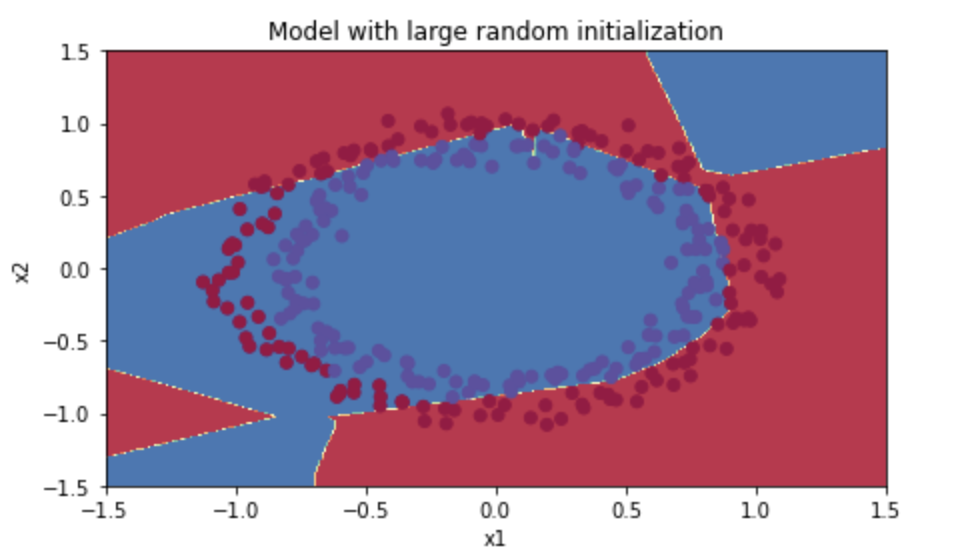
• Train Accuracy: 83%

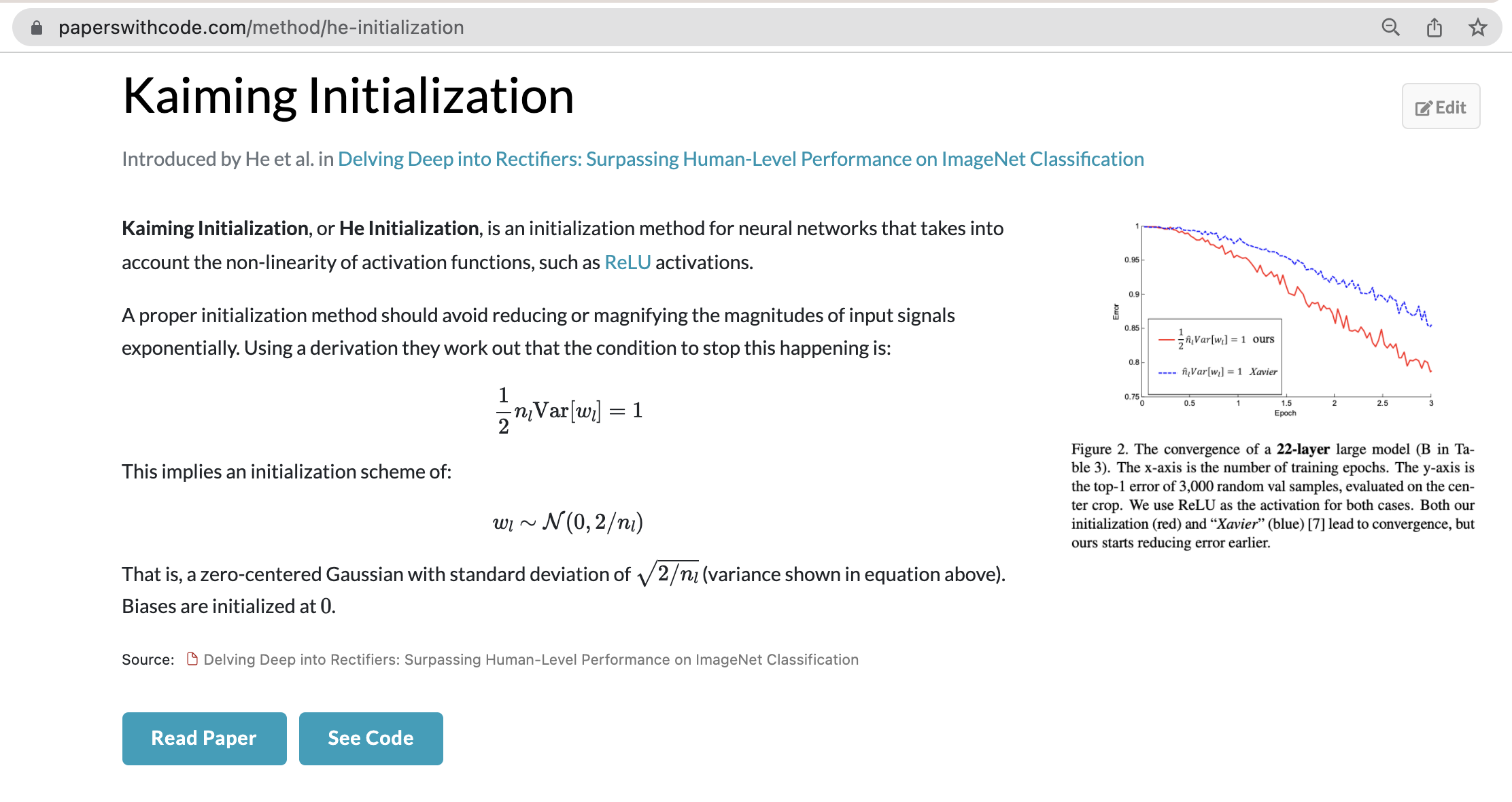
He Initialization

This initializes the weights to random values scaled according to a paper by He et al., 2015.

• parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*math.sqrt(2./layers_dims[l-1])
• parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))*math.sqrt(2./layers_dims[l-1])

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def initialize_parameters_he(layers_dims):

    np.random.seed(3)
    parameters = {}
    L = len(layers_dims) - 1 # integer representing the number of layers
    import math
    for l in range(1, L + 1):

        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*math.sqrt(2./layers_dims[l-1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))*math.sqrt(2./layers_dims[l-1])

    return parameters

Output:

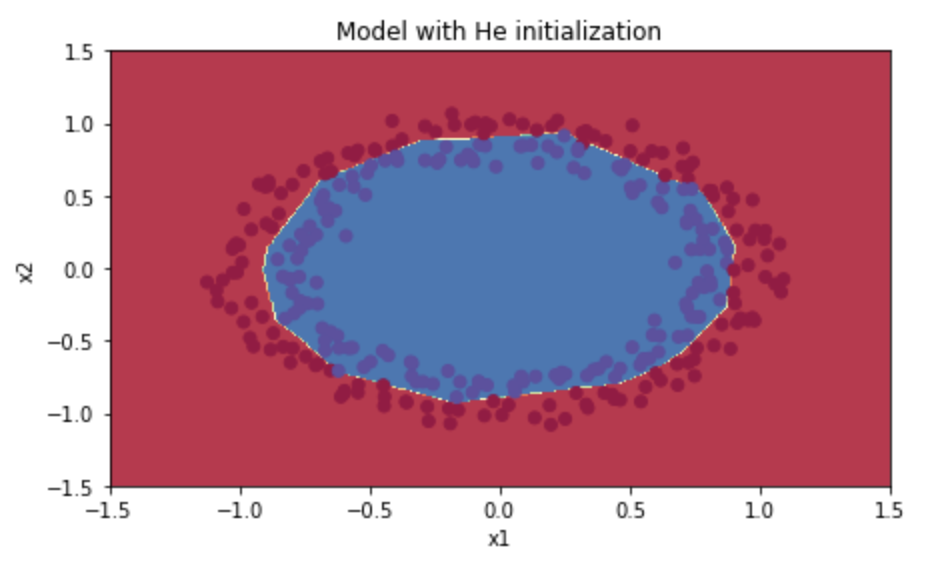
• Train Accuracy: 99%

2. Gradient Check

• Don’t use in training - ONLY to debug
• If algorithm fails Gradient Check, look at components to try to identify bug
• Remember Regularization
• Doesn’t work with Dropout
• Run at Random Initialization; perhaps again after some training